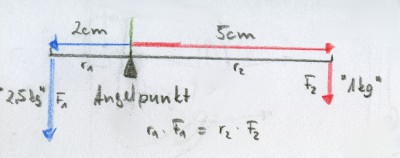
Nachdem mein Artikel über die Hebelwirkung einer Kandare zahlreiches und durchweg positives Feedback bekommen habe – Danke an dieser Stelle – habe ich auch ein 10-seitiges PDF bekommen, welches einige Punkte, die ich in meiner Ausarbeitung der Einfachheit halber ausgelassen habe, erläutert.
Ingo Driever hat sich mit den veränderten Kraftverhältnissen bei einer angewinkelten Kandare und der Springkandare beschäftigt. Er berücksichtigt dabei auch, dass der Zügel nicht wie in meiner Ausarbeitung waagerecht wirkt (also 90° zur Senkrechten der Pferdenase), sondern eher in einem Winkel von 30° zur Waagerechten.
Anmerkungen meinerseits sind kursiv gekennzeichnet.
Die angewinkelte Kandare
Bei der angewinkelten Kandare muss Zugrichtung und Anzugwinkel betrachtet werden. Selbst bei einem an die Senkrechte gestellten Pferd ist die Zugrichtung normalerweise oberhalb der Waagerechten (Wer hat seine Hände schon am Oberschenkel).
Ist bei einer 30° gebogenen Kandare die Zugrichtung 30° nach oben (rechter Winkel zwischen Unterbaum und Zügel), wirkt der volle Hebel des Unterbaums. Die wirksame Länge des Unterbaums verkleinert sich nicht, sondern die des Oberbaums. Bezogen auf die ursprüngliche Berechnung bedeutet das:
wirksame Länge Unterbaum – 5,0cm
wirksame Länge Oberbaum – 1,73cm
Also ein Verhältnis von 5:1,73 was 2,89kg bei 1kg Zuggewicht entspricht.
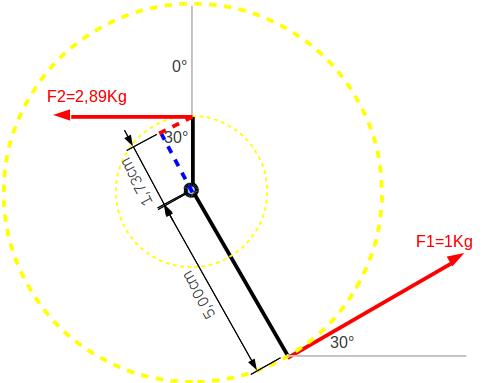
Wenn wir aus dieser Ruhestellung nun anziehen würden, würde der wirksame Hebel des Unterbaums immer weiter abnehmen. Gleichzeitig würde der wirksame Hebel des Oberbaums zunehmen, bis er bei 30° seinen höchsten Wert erreicht hat.

Würden wir jetzt weiter anziehen, würde auch der wirksame Hebel des Unterbaums wieder kleiner werden.

Oder anders gesagt: im Gegensatz zur geraden Kandare ändert sich das Verhältnis von Ober- zu Unterbaum bei der gebogenen Kandare je nach der Winkelung der Kandare, Aufrichtung des Pferdes, Höhe der Reiterhand, Anzugwinkel und je nach dem, wie weit das Pferd an die Senkrechte kommt.
In unserem Beispiel würde die Hebelwirkung der Kandare also bei vermehrtem Anzug (und vermehrter Kraft), immer weiter abnehmen.
Beispiel: Pferd in der Senkrechten und Zugrichtung 30° über der Waagerechten
| Anzugwinkel bzgl. Oberbaum |
wirksame Länge Unterbaum |
wirksame Länge Oberbaum |
resultierende Kraft bei 1kg Anzug |
| 0° | 5,00 cm | 1,73 cm | 2,89 kg |
| 10° | 4,92 cm | 1,88 cm | 2,62 kg |
| 20° | 4,70 cm | 1,97 cm | 2,39 kg |
| 30° | 4,33 cm | 2,00 cm | 2,17 kg |
| 45° | 3,54 cm | 1,93 cm | 1,83 kg |
Die Springkandare
Um den komplizierten Kraftverlauf der Springkandare zu verstehen kann man sie am besten gedanklich aufteilen.
Wir stellen uns eine Lampe vor, die an zwei gleichlangen Seilen von der Decke hängt. Die Lampe wiegt 1 kg. Also zieht an den beiden Haltepunkten A und B je 0,5 Kg.
Wenn man die Zugrichtung der Lampe rückwärts verlängert, trifft diese genau in der Mitte die Verbindungslinie von A nach B.

Wir verändern jetzt die Seillängen so, dass die Lampe unter einem Punkt, der der 1m von A und 2 m von B entfernt ist, hängt.
Die Verlängerung der Zugrichtung der Lampe teilt die Entfernung A zu B im Verhältnis 1/3 zu 2/3. Genauso verhält es sich mit den Kräften an den Punkten A und B. Wichtig dabei ist, dass die für die Bestimmung der Last maßgeblich Entfernung auf der jeweils gegenüberliegenden Seite zu suchen ist (grün, blau).

Hängen wir nun unsere Lampe ab und und bringen beide Seile wieder auf die gleiche Länge. Nun ziehen mit 1 kg an dem Seil, aber nicht nach unten, sonder schräg zur Seite. Genau so, dass die Verlängerung unserer Zugrichtung die Linie zwischen A und B 1/3 zu 2/3 teilt. Wir haben nun wieder die gleiche Kräfteverteilung wie im letzten Beispiel.

Nun ziehen wir noch schräger, so dass die Verlängerung der Zugrichtung auf einem Punkt 43 cm hinter Punkt A rauskommt. An Punkt A würden wir jetzt mit 1Kg ziehen, während das Seil zu Punkt B durch hängen würde.
Tauschen wir aber die Seile gegen Stahlstangen, würde wir an Punkt B einen Druck nach oben ausüben, während wir an Punkt A nicht mehr mit einem ganzen Kilogramm ziehen würden.
Wichtig: das Grundmaß für die Berechnung ist die Entfernung von Punkt B zu dem Punkt, wo die Verlängerung der Zugrichtung die Verlängerung von A nach B schneidet.
Rechnung:
p(A) = 3m : 3,43m x 100 = 87,463556851%, gerundet 87%
PW(A) = 87% :100 x 1kg = 0,87kg
p(B) = 0,43m : 3,43m x 100 = 12,536443149%, gerundet 13%
PW(B) = 13% : 100 x 1Kg = 0,13Kg

Noch einmal zurück zum vorigen Beispiel. Ersetzen wir unsere Decke nun mal durch eine Hebelwaage, deren Achse 2m von A Punkt und 1m von B Punkt liegt (schwarz).
Wir wollen wissen, welche Kraft an einem Punkt C ankommt, der 0,5m hinter Punkt B liegt. Da unsere Kräfte aber gegeneinander und dazu noch an unterschiedlich langen Hebelarmen wirken, müssen wir erst herausfinden wie viel Kraft denn überhaupt wirkt.
Der beste Weg dies zu errechnen ist der über das Drehmoment (M). Das Drehmoment ist eigentlich nichts anderes als ein um die Hebellänge bereinigte Hebelkraft.
Drehmoment = Kraft x Hebelarm oder Kraft x Radius (M = F x r).
Normalerweise wird das Drehmoment in Newton-Meter Nm (1Kg = 9,81Nm) gerechnet, aber hier nehmen wir einfach kg/m.
Rechnung:
M(A) = 0,77kg x 2m = 1,54kg/m
M(B) = 0,33kg x 1m = 0,33kg/m
Da die Kräfte in entgegengesetzte Richtungen wirken müssen wir sie voneinander subtrahieren.
M(gesamt) = 1,54kg/m – 0,33kg/m = 1,21kg/m
Um die Kraft an C herauszufinden müssen wir die Formel umstellen.
M = F x r <=> F = M : r
Rechnung
F2 = 1,21kg/m : 1,5m = 0,75kg
Anmerkung: Dies entspricht in etwa einer Springkandare, bei der der Zügel im oberen Schlitz verschnallt ist und der Zügel nicht waagerecht sondern in ca. 30° nach oben wirkt (siehe folgendes Bild). Das D der Springkandare entspricht dem Dreieck aus A, B und dem Zugpunkt, Punkt C ist die Aufhängung am Genickriemen, die Achse entspricht der Position des Mundstücks.

Rechnen wir dies noch mal für das Beispiel, bei dem die Verlängerung der Zugrichtung 0,43m hinter Punkt A lag. Da hier beide Drehmomente in die selbe Richtung wirken, müssen wir sie hier addieren.
Rechnung:
M(A) = 0,87kg x 2m = 1,74kg/m
M(B) = 0,13kg x 1m = 0,13kg/m
M(ges) = 1.74kg/m + 0,13kg/m = 1,87kg/m
F2 = 1,87kg/m : 1,5m = 1,25kg
Anmerkung: Dies entspricht einer Springkandare, bei der der Zügel im unteren Schlitz verschnallt ist.
Und nun noch einmal, wenn die Verlängerung der Zugrichtung exakt auf Punkt A liegt.
M(A) = 1kg x 2m = 2kg/m
F = 2kg/m :1,5m = 1,33kg
Und siehe da, die maximale Kraft die wir mit 1kg Zug an Punkt C (Anm.: Aufhängung der Kandare) erzeugen können, ist exakt das Verhältnis von Kraftarm zu Lastarm ( 2m : 1,5m = 1,33).
Also gilt für die Springkandare, wie für jede gerade Kandare, der maximale Hebel ergibt sich aus dem Verhältnis von Ober- zu Unterbaum. Entscheidend für die tatsächliche Kraftentwickelung ist der Punkt, an dem die Verlängerung des Zügels auf den Baum trifft. Dieser wird natürlich davon beeinflusst, ob man den Zügel oben oder unten verschnallt, aber genauso von der Aufrichtung des Pferdes, Höhe der Reiterhand, Anzugwinkel und je nach dem wie weit das Pferd an die Senkrechte kommt.
Fazit
Nun noch meine persönliche Meinung zum Thema Rechnen rund um die Kandare. Ich habe den ganzen Hebel Kram, schon von wirklich renommierten Reitern/Reitlehrern gehört und gelesen (z.B. Branderup im Buch „Reiten auf Kandare“).
Nur was sagen diese ganze Hebelberechnungen aus? Eigentlich gar nichts. Es wird immer wieder der Fehler gemacht die Zügelkraft einer Trense über die Hebelgesetze mit der einer Kandare zu vergleichen zu wollen. Das ist Äpfel mit Birnen zu vergleichen, da wir die ganze Zeit die Kraft berechnet haben, die am dem Punkt wirkt, an dem die Kandare am Kopfstück befestigt ist.
Die Antwort mit wie viel Kraft eine Kandare nun auf das Maul des Pferdes wirkt, habe ich noch nirgendwo gefunden.
Dabei ist die Lösung eigentlich ganz simpel. Dazu verlassen wir die Mechanik, die Lehre von Kräften in der Bewegung, und wenden uns der Statik, der Lehre von Lasten bei ruhenden Körpern, zu. Das heißt, wir betrachten nur den Augenblick in dem sich die Kräfte aufheben und die Kandare sich in einer festen Position befindet.
Wir stellen uns jetzt eine asymmetrische Balkenwaage vor (1/3 zu 2/3 Teilung), die wir in der Hand halten. An die Wage hängen wir an die einen Seite 1 kg und an der anderen Seite 2kg. Der Balken ist nun im Gleichgewicht. Wir würden jetzt 3 kg in der Hand halten (plus Eigengewicht der Waage).
Wenn die Waage jetzt nicht in unserer Hand wäre, sondern auf einem Sockel stünde, würde sie mit 3kg auf den Sockel drücken.

Nun zurück zur Kandare, wir ziehen mit 1Kg am Zügel und erzeugen an der Gegenseite eine Kraft von 2kg. Der Hebel wird sich so lange bewegen bis Kinnkette und Genickstück eine Gegenkraft von 2kg aufgebaut haben. Die Kräfte heben sich in diesem Moment auf. Der Hebel bleibt in diesem Winkel stehen, und solange sich nichts ändert, wird die Kandare in dieser Stellung bleiben.
Wenn wir genau diesen Augenblick betrachten, hängen die Zügelkraft (1kg) und die Gegenkraft von Kinnkette und Genickstück (2kg) als Lasten an der Waage. Auf den Sockel, also das Maul des Pferdes, wirkt jetzt eine Last von 3kg.
Hinweis: Wie sich die Kraft von 2kg genau zwischen Kinnkette und Genickstück verteilt, würde den Rahmen dieses Aufsatzes sprengen. Eventuell mal in einem anderen Aufsatz … später.

Meine Theorie
Leider hat die Betrachtung der Kandare als zweiseitiger Hebel in der Realität einen kleinen Schönheitsfehler. Die Achse in unseren Berechnungen, im Maul des Pferdes, ist nicht fest gelagert sondern sie bewegt sich.
Eventuell müssen wir für die Berechnung der Kraft auf das Maul das System Kandare als einseitigen Hebel betrachten. Dann wäre das Auge am Oberbaum unsere Achse und die gesamte Länge der Kandare unser Hebelarm. Dann hätte unser Hebel nun ein Verhältnis von 3/4 zu 1/4 anstelle von 2/3 zu 1/3.

Leider ist auch das Auge des Oberbaums nicht wirklich fest gelagert. In der Realität haben wir es also mit einem System zu tun, dessen Achsen sich verschieben und welches vermutlich teils als ein- und teils als zweiseitiger Hebel wirkt (vgl. Wikipedia Hebel Ruder).
Eventuell verhält es sich ja so:
1. Bei beginnendem Anzug sind die Kinnkette und Genickstück entspannt. Die Gebissstange hebt sich wohl kaum oder gar nicht. Die Hebelachse liegt auf Höhe der Gebiss-Stange.
2. Bei steigendem Anzug beginnt die Kinnkette zu wirken, um ein Verschieben des Oberbaum-Endes nach vorn zu behindern. Auf das Genickstück entsteht Zug und die Gebiss-Stange drückt sich vermehrt in die Maulwinkel und Kiefer. Eventuell beginnt sich Hebelachse zu verschieben.
3. Bei weiter steigendem Anzug behindert die Kinnkette immer mehr das Ausweichen des Oberbaum-Endes nach vorn. Es entsteht immer mehr Zug auf das Genickstück. Gleichzeitig drückt sich die Gebiss-Stange immer mehr in die Maulwinkel und Kiefer. Die Kandare beginnt zwischen Oberbaum-Ende und Gebissstange zu rotieren. Die Hebelachse verschiebt sich also. Für die Gebissstange wird die Kandare zum einseitigen Hebel. Bezogen auf das Oberbaum-Ende wird das Verhältnis Kraft- zu Lastarm immer größer.
Die Verteilung dieser Kräfte unter realen Bedingungen zu berechnen dürfte ein ziemlich schwieriges Unterfangen werden. Eventuell lässt es sich gar nicht berechnen, sondern nur messen. Dies wäre sicherlich ein spannendes Thema für die Diplomarbeit eines Biomechanik-Studenten.
Bleibt nur noch zu sagen – frei nach Bent Branderup – „Ein Stück Stahl im Maul eines Pferdes ist nie weich“ und „die Härte eines Gebisses liegt in der Reiterhand“.

„Um die Ecke gedacht – Die Physik in der Kandare II“ von Ingo Driever steht unter einer Creative Commons Namensnennung – Weitergabe unter gleichen Bedingungen 3.0 Deutschland Lizenz.