Ausgehebelt – Die Physik in der Kandare

Gleich vornweg: Ich bin kein Physiker und beim Gebrauch einer Kandare wirken weit mehr Faktoren als hier beschrieben. Des Weiteren versuche ich das Thema möglichst einfach darzustellen, weshalb ich auf korrekte Maßeinheiten und maßstabsgerechte Zeichnungen verzichte.

Vor Kurzem hatte ich eine recht interessante, bisweilen anstrengende Diskussion auf Facebook zum Thema „Kandare“. Konkret ging es um S-Kandaren und es stand die Behauptung im Raum, S-Kandaren wären um ein vielfaches schärfer als normale Kandaren. Da bin ich hellhörig geworden, weil mir diese pauschale Behauptung merkwürdig vorkam. Es stellte sich heraus, dass mein Gegenüber dem Irrglauben aufgesessen war, dass eine S-Kandare einen längeren Unterbaum hat als gerade Kandaren – wickelt man das S ab, wäre der Hebel länger und somit die ausgeübte Kraft höher.
Dem ist nicht so, denn der Hebelarm ist klar definiert als Abstand vom Angelpunkt zum Angriffspunkt. Die Form des Hebels ist dabei absolut unerheblich und wirkt sich höchstens auf das Eigengewicht des des Hebels aus. Dieser Nebenfaktor soll hier aber ausgeblendet sein.

Eine Kandare ist grundsätzlich ein zweiseitiger Hebel, wobei bei einer Dressurkandare der Kraftarm (also der Arm auf den Kraft ausgeübt wird) der Unterbaum von 5-7 cm ist und der Lastarm (also der Arm auf den die Kraft/Last wirkt) der Oberbaum von ca. 2 cm ist. In den folgenden Beispielen gehe ich stets von einem Verhältnis von 2cm Oberbaum (blau) zu 5cm Unterbaum (rot) aus. Das entspricht einer Baby-Kandare.

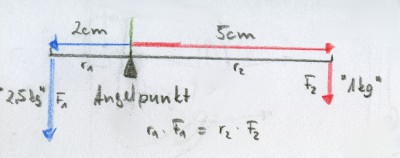
Für einen zweiseitigen Hebel gilt das Gesetzt „Kraft mal Kraftarm gleich Last mal Lastarm“. Als Formel: F₁ x r₁ = F₂ x r₂ wobei F die Kraft ist und r die Länge des Hebels. Im Falle einer Kandare mit obengenannten Längen gilt demnach, dass am Oberbaum die 2,5fache Kraft wirkt wie am Zügel. Ziehe ich also am Kandarenzügel mit 1kg wirken auf Kinnkette und Genickriemen (jeweils am Angriffspunkt des Oberbaum) 2,5kg. Die Rechnung sieht wie folgt aus:

Im Vergleich nun eine Dressurkandare gegen eine S-Kandare. Wie man sieht, ist unabhängig von der S-Form der Kraftarm bei beiden Kandaren gleich. Da der Oberbaum in beiden Fällen gleich lang ist, wirkt die gleiche Kraft. Im Gebrauch macht es demnach keinen Unterschied, ob man eine Dressur- oder S-Kandare verwendet. Letztere sieht vielleicht gefälliger aus.

Die Form des Unterbaums wird erst relevant, wenn der Angriffspunkt sich nicht in einer Linie mit dem Oberbaum befindet. In der Physik spricht man dann von einem Winkelhebel. Das Hebelgesetz, wie oben beschrieben, bleibt grundsätzlich gleich, es ändert sich quasi die Definition des Hebelarms.
Im Falle der Kandare kann man davon ausgehen, dass die gedachte Grundlinie in Verlängerung des Oberbaums (also analog zur Dressurkandare) verläuft und der Unterbaum nach hinten gebogen ist. Die Zugkraft wirkt senkrecht auf die Grundlinie. Es ergibt sich also zwischen Grundlinie, Unterbaum und Zugrichtung ein rechtwinklinges Dreieck und an der Ecke des rechten Winkels befindet sich der eigentliche Angriffspunkt, wie in der folgenden Abbildung dargestellt ist.

Ausgehend von einem Unterbaum von 5cm, einem Winkel von 30°, in dem der Unterbaum nach hinten gebogen ist, und einer Zugkraft von 1kg, ergibt sich für den eigentlichen Angriffspunkt und somit Hebelarm eine Länge von 4,33cm und eine ausgeübte Kraft von 2,16kg:

Ein nach hinten gebogener Unterbaum wirkt bei gleicher Länge demnach weniger stark. Zur Veranschaulichung hier nochmal der Vergleich einer „geraden“ S-Kandare und einer nach hinten gebogenen.

Der gleiche Effekt stellt sich bei einer Springkandare (Kimblewick) bzw. einer Friesenkandare ein. Auch hier ist der Unterbaum nach hinten gebogen und der Hebelarm demnach kürzer. Es gibt auch die Variante, dass der Unterbaum nach vorn gebogen ist. In diesem Fall greift dieselbe Rechnung und somit diegleiche Krafteinwirkung. Der Unterschied liegt in dem Weg, den der Hebel in Abhängkeit von der Kinnkette zurücklegen kann, aber dazu am Ende mehr.
Die Sprinkandare und Friesenkandare bieten die Möglichkeit, den Zügel auf selber Höhe wie das Mundstück zu verschnallen (orange). Der Winkel zur Grundlinie (Verlängerung des Oberbaums) beträgt somit 90°. Als Resultat ist der Hebelarm 0cm lang, was grafisch sehr gut deutlich wird:

Wie in der Zeichnung schon skizziert, bedeutet dies, dass keinerlei Kraft auf den Oberbaum wirkt (= 0kg). Die Zugkraft von 1kg wirkt somit direkt auf den Angelpunkt also das Mundstück und in letzter Instanz auf die Zunge. Eine Hebelwirkung exisitiert hier nicht.

Fazit

Das Fazit ist relativ einfach: Um so kürzer der Unterbaum, desto weniger Kraft wirkt auf den Oberbaum. Ein nach hinten gebogener Unterbaum wirkt kürzer und somit mit weniger Kraft als ein gleichlanger, gerader Unterbaum.

So weit so gut – weitere Faktoren

So einfach das Fazit scheint, ist es natürlich nicht. Ich bin in diesem Ausführungen vom Idealzustand ausgegangen und bin einzig auf die wirkende Kraft eingegangen. Ein wichtiger Faktor bei der Unterbaumlänge, der noch nicht zur Sprache kam, ist die „Geschwindigkeit“ mit der die Kraft ankommt.

Um eine Kandare beispielsweiese in einen Wirkungswinkel von 45° zu bringen, muss bei einem 5cm langen Unterbaum ein Weg von 3,5cm zurückgelegt werden, bei einem 7cm langen Baum ein Weg von 4,9cm. Bei jeweils gleich starker Krafteinwirkung und – geschwindigkeit, wirkt bei einem kurzen Unterbaum die Kraft quasi „eher“. Es gilt also auch: Um so kürzer der Unterbaum, desto schneller wirkt die Zugkraft.
Bei der Frage, ob kurzer oder langer Unterbaum, liegt die Antwort also irgendwo in der Mitte, denn ein kurzer, direkter Unterbaum ist nicht zwangsläufig besser als ein langer, verzögerter Unterbaum. Dies gilt es abzuwägen.

Ebenso von Bedeutung ist die Verschnallung der Kinnkette. Idealerweise sollte die Kinnkette so verschnallt sein, dass Kandare und Zügel einen 90°-Winkel bilden – zur Orientierung auch: die Kandare im Anschlag bildet einen Winkel von 45° zur Kandare in der Ruheposition. Ist die Kette enger verschnallt (also < 45°), spricht man von der strotzenden Kandare. Die Kinnkette wirkt dann sehr unvermittelt und schnell auf den Laden und bei zunehmender Kraft bildet sich quasi ein Knebel zwischen Kinnkette und Mundstück. Ist die Kinnkette zu lose eingeschnallt (also > 45°), spricht man von der durchfallenden Kandare. Nimmt man die Kandarenzügel auf, wirkt die Kinnkette erst sehr spät, so dass die Kandare fast waagerecht steht. Die Hebelwirkung tendiert also gen 0.
Bei einer nach vorn gebogenen Kandare ähnelt der Effekt eher der einer strotzenden Kandare. Um einen Wirkungswinkel von 45° zu erreichen, muss wesentlich mehr Weg zurückgelegt werden (angenommener Zügel), wobei gleichzeitig der Druck über die Kinnkette sehr früh und mit mehr Zügelaufnahme immer stärker erfolgt.

Bei der gesamten Betrachtung habe ich, wie oben erwähnt, einige Punkte außer Acht gelassen, die ebenfalls Auswirkung auf das Gesamtkonstrukt haben. So ist auch das Eigengewicht der einzelnen Abschnitte der Kandare, Form des Mundstückes (Zungenfreiheit positioniert sich parallel zum Unterbaum), Zügelführung (Handhöhe variiert den Wirkwinkel der Zugkraft) oder der Elevatoreffekt (Anheben des Mundstückes im Pferdemaul) von Bedeutung.

Zur Geschichte und Wirkweise einer Kandare kann ich als Lektüre „Reiten auf Kandare“ von Bent Branderup empfehlen.

Nice to know

Und wer sich schon immer mal gefragt hat, wozu eine Dressurkandare in der Mitte des Unterbaums je eine Öse hat: Diese Öse ist zum Verschnallen des sogenannten Scherriemen gedacht, der auch durch den mittigen Ring der Kinnkette geführt wird. Der Scherriemen soll verhindern, dass das Pferd den Unterbaum ins Maul nimmt. Bei zurückgebogenen Bäumen ist dieser Riemen überflüßig.